We investigate how to use an ![]() factorization with the classical lsqr routine for solving overdetermined sparse least squares problems.
Usually
factorization with the classical lsqr routine for solving overdetermined sparse least squares problems.
Usually ![]() is much better conditioned than
is much better conditioned than ![]() . Thus iterating with
. Thus iterating with ![]() instead of
instead of ![]() results in faster convergence.
Numerical experiments using Matlab illustrate the good behavior of our
algorithm in terms of storage and convergence.
This paper explores a preliminary shared memory implementation using
SuperLU factorization.
results in faster convergence.
Numerical experiments using Matlab illustrate the good behavior of our
algorithm in terms of storage and convergence.
This paper explores a preliminary shared memory implementation using
SuperLU factorization.
We consider the overdetermined full rank LLS problem
with other sparse linear systems, preconditoning techniques based on
incomplete factorizations can improve convergence. One method to
precondition the normal equations (![]() ) is to perform an
incomplete Cholesky decomposition of
) is to perform an
incomplete Cholesky decomposition of ![]() (e.g., RIF preconditioner,
Benzi, 2003).
(e.g., RIF preconditioner,
Benzi, 2003).
When ![]() and its Cholesky factorization are denser than
and its Cholesky factorization are denser than ![]() , it is
natural to wonder if the
, it is
natural to wonder if the ![]() factorization of
factorization of ![]() can be used in solving
the least squares problem. In this paper we use an
can be used in solving
the least squares problem. In this paper we use an ![]() factorization of
the rectangular matrix
factorization of
the rectangular matrix
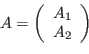 where
where ![]() is unit lower trapezoidal and
is unit lower trapezoidal and ![]() is upper triangular.
For the nonpivoting case, the normal equations (
is upper triangular.
For the nonpivoting case, the normal equations (![]() ) become
) become
Least squares solution using ![]() factorization has been explored by
several authors. Peters and Wilkinson (1970) and Björck and Duff (1980)
give direct methods. This work follows Björck and Yuan (1999) using
conjugate gradient methods based on
factorization has been explored by
several authors. Peters and Wilkinson (1970) and Björck and Duff (1980)
give direct methods. This work follows Björck and Yuan (1999) using
conjugate gradient methods based on ![]() factorization, an approach worth
revisiting because of the recent progress in sparse
factorization, an approach worth
revisiting because of the recent progress in sparse ![]() factorization.
The lsqrLU (2015) algorithm presented here uses a lower trapezoidal
factorization.
The lsqrLU (2015) algorithm presented here uses a lower trapezoidal ![]() returned from a direct solver package. Here we use an
returned from a direct solver package. Here we use an ![]() factorization from shared memory SuperLU (X. LI 2005), comparing
iteration with
factorization from shared memory SuperLU (X. LI 2005), comparing
iteration with ![]() to the
to the ![]() iteration suggested by Saunders.
Because other direct solver packages offer scalable sparse
iteration suggested by Saunders.
Because other direct solver packages offer scalable sparse ![]() factorizations, it appears likely that the algorithm used here can also
be used to solve larger problems.
The rate of linear convergence for CG iterations on the normal equations is
factorizations, it appears likely that the algorithm used here can also
be used to solve larger problems.
The rate of linear convergence for CG iterations on the normal equations is
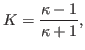
where