


Next: Bibliography
Andrei Draganescu
Optimal-order multigrid preconditioners for linear systems arising in the semi-smooth Newton solution of certain PDE-constrained optimization problems
Department of Mathematics and Statistics
UMBC
1000 Hilltop Circle
Baltimore
MD 21250
draga@umbc.edu
Jyoti Saraswat
We present a new technique for constructing multigrid preconditioners
arising in the semi-smooth Newton solution process of optimization
problems of the form
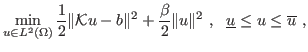 |
(1) |
where
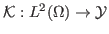 is a bounded linear operator, with
the embedding
is a bounded linear operator, with
the embedding
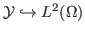 being compact, and
being compact, and
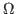 is a bounded Lipschitz domain. The problem (1)
can be regarded as the reduced form of a PDE-constrained optimization
problem
with
is a bounded Lipschitz domain. The problem (1)
can be regarded as the reduced form of a PDE-constrained optimization
problem
with
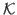 being the solution operator of a PDE (for example,
being the solution operator of a PDE (for example,
 ).
).
For a piecewise constant discretization of the control space 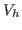 , each
semi-smooth Newton (outer) iteration requires the solution of a linear
system whose matrix is a principal submatrix of
, each
semi-smooth Newton (outer) iteration requires the solution of a linear
system whose matrix is a principal submatrix of
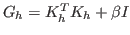 ,
where
,
where 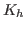 is the matrix representing the discretization of
is the matrix representing the discretization of
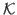 , and
, and 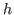 is the mesh size.
In a large-scale context these (inner) linear systems are solved using
preconditioned conjugate gradient. An earlier technique [1]
produced a multigrid preconditioner
is the mesh size.
In a large-scale context these (inner) linear systems are solved using
preconditioned conjugate gradient. An earlier technique [1]
produced a multigrid preconditioner  for
for  that satisfies, under
reasonable conditions,
that satisfies, under
reasonable conditions,
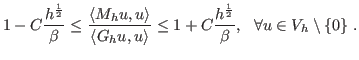 |
(2) |
As a result of (2), the number of inner linear
iterations needed to solve the system at each outer iteration decreases
with
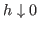 . While this result is interesting from a theoretical
point of view (and qualitatively consistent with the behavior of the
preconditioner for the full system), its practicality is limited by the
suboptimal factor
. While this result is interesting from a theoretical
point of view (and qualitatively consistent with the behavior of the
preconditioner for the full system), its practicality is limited by the
suboptimal factor 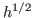 in (2).
in (2).
The new technique, relying on constructing larger coarse spaces than
before, produces multigrid preconditioners  that are able to capture
the character of the
operator
that are able to capture
the character of the
operator  in an optimal way, namely we have
in an optimal way, namely we have
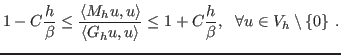 |
(3) |



Next: Bibliography
Copper Mountain
2014-02-24
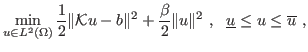
![]() , each
semi-smooth Newton (outer) iteration requires the solution of a linear
system whose matrix is a principal submatrix of
, each
semi-smooth Newton (outer) iteration requires the solution of a linear
system whose matrix is a principal submatrix of
![]() ,
where
,
where ![]() is the matrix representing the discretization of
is the matrix representing the discretization of
![]() , and
, and ![]() is the mesh size.
In a large-scale context these (inner) linear systems are solved using
preconditioned conjugate gradient. An earlier technique [1]
produced a multigrid preconditioner
is the mesh size.
In a large-scale context these (inner) linear systems are solved using
preconditioned conjugate gradient. An earlier technique [1]
produced a multigrid preconditioner ![]() for
for ![]() that satisfies, under
reasonable conditions,
that satisfies, under
reasonable conditions,
![]() that are able to capture
the character of the
operator
that are able to capture
the character of the
operator ![]() in an optimal way, namely we have
in an optimal way, namely we have