Next: About this document ...
Jack C.H. Blake
An asymptotic analysis of preconditioned linear systems arising from discretisations of the transport equation within a diffusive regime.
Mathematical Sciences
University of Bath
Claverton Down
Bath
UK
BA2 7AY
J.C.H.Blake@bath.ac.uk
Ivan G. Graham
Alastair Spence
An important problem in applied nuclear physics is that of efficiently
solving the neutron transport equation. In 5D (three spatial and two
angular dimensions) this equation is given by
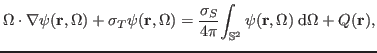 |
(1) |
where
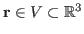 and
and
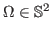 (the unit sphere in
(the unit sphere in
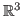 ). Here:
). Here:
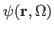 denotes the neutron flux, which is the
density of neutrons passing through a unit space at
denotes the neutron flux, which is the
density of neutrons passing through a unit space at
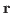 in
direction
in
direction 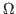 per unit time;
per unit time; 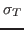 and
and 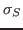 are constants
which describe the different interactions a neutron can undergo; and
are constants
which describe the different interactions a neutron can undergo; and
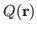 denotes the neutron source, and is a known
non-fission source term, isotropic in angle, of neutrons from position
denotes the neutron source, and is a known
non-fission source term, isotropic in angle, of neutrons from position
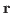 . This equation is subject to suitable boundary conditions on
the boundary of
. This equation is subject to suitable boundary conditions on
the boundary of 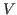 .
.
Due to its high dimension, (1) results in huge linear systems
when discretised, and we are interested in fast methods for solving
these. In this talk we will look at one solution method in the context of
a 2D model problem, with one spatial dimension,
![$ x \in [0,1]$](img12.png) , and one
angular dimension,
, and one
angular dimension,
![$ \mu \in [-1,1]$](img13.png) . Under this restriction the transport
equation is given by
. Under this restriction the transport
equation is given by
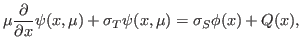 |
(2) |
where 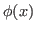 is called the scalar flux and is defined as
is called the scalar flux and is defined as
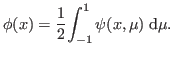 |
(3) |
Along with this we specify boundary conditions
A fixed-point iteration based upon repeatedly solving (2) for
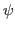 (with the right hand side of (2) formed from the
previous value of
(with the right hand side of (2) formed from the
previous value of 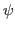 ) is known as source iteration. This
suffers potentially very slow convergence when the ratio
) is known as source iteration. This
suffers potentially very slow convergence when the ratio
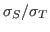 is close to 1, a situation often referred to as working
within a diffusive regime. Using an asymptotic analysis of
(2) and its solution, it is well known that a specific
diffusion equation can be derived, given by
is close to 1, a situation often referred to as working
within a diffusive regime. Using an asymptotic analysis of
(2) and its solution, it is well known that a specific
diffusion equation can be derived, given by
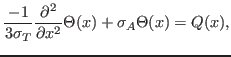 |
(4) |
with associated boundary conditions, where 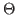 approximates
approximates  as described by Habetler & Matkowsky [G. Habetler & B. Matkowsky, 75]
and later Jin & Levermore [S. Jin & D. Levermore, 91]. This
approximation can be used to accelerate source iteration using ideas
first proposed by Kopp [H.J. Kopp, 1963], leading to a scheme known as
diffusion synthetic acceleration (DSA). Using (4), DSA
can be defined as in [E. Larsen, 1984] as an accelerated `2-step'
iterative process. Faber & Manteuffel [V. Faber & T.A. Manteuffel,
1988] showed that this `2-step' DSA is equivalent to a preconditioned
fixed-point iterative scheme.
as described by Habetler & Matkowsky [G. Habetler & B. Matkowsky, 75]
and later Jin & Levermore [S. Jin & D. Levermore, 91]. This
approximation can be used to accelerate source iteration using ideas
first proposed by Kopp [H.J. Kopp, 1963], leading to a scheme known as
diffusion synthetic acceleration (DSA). Using (4), DSA
can be defined as in [E. Larsen, 1984] as an accelerated `2-step'
iterative process. Faber & Manteuffel [V. Faber & T.A. Manteuffel,
1988] showed that this `2-step' DSA is equivalent to a preconditioned
fixed-point iterative scheme.
In this talk we use the asymptotic approach to derive an explicit
convergence rate (in terms of an asymptotic expansion coefficient) for
the preconditioned source iteration of Faber & Manteuffel. This provides
a simple way to analyse the `2-step' DSA method, reinforcing the analysis
of Faber & Manteuffel. Next we use the asymptotic approach to look at
the convergence of preconditioned Krylov methods. Numerical results will
be given to support our analysis.



Next: About this document ...
Copper Mountain
2014-02-24
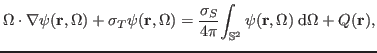
![]() , and one
angular dimension,
, and one
angular dimension,
![]() . Under this restriction the transport
equation is given by
. Under this restriction the transport
equation is given by