Introduction.
In this work we present a new efficient calculation method for the far
field amplitude patterns that arise from scattering problems governed by
the ![]() -dimensional Helmholtz equation. The calculation of the far field
mapping is typically a two step process. First a Helmholtz problem with
absorbing boundary conditions (PML, ECS) is solved on a finite numerical
box covering the object of interest. In the second step a volume integral
over the Green's function involving the numerical solution yields the
angular dependency of the far field amplitude. The main computational
bottleneck generally lies within the first step, since it requires a
suitable (iterative) method for the solution of a high dimensional
indefinite Helmholtz system.
-dimensional Helmholtz equation. The calculation of the far field
mapping is typically a two step process. First a Helmholtz problem with
absorbing boundary conditions (PML, ECS) is solved on a finite numerical
box covering the object of interest. In the second step a volume integral
over the Green's function involving the numerical solution yields the
angular dependency of the far field amplitude. The main computational
bottleneck generally lies within the first step, since it requires a
suitable (iterative) method for the solution of a high dimensional
indefinite Helmholtz system.
Preconditioned Krylov subspace methods are currently among the most efficient numerical algorithms for the solution of high dimensional positive definite systems. A generalization of this approach led to the development of the Complex Shifted Laplacian (CSL) preconditioner, proposed in [1] as an effective Krylov subspace method preconditioner for Helmholtz problems. The key idea behind CSL is the formulation of a perturbed Helmholtz problem which includes a complex valued wave number. This implies a damping in the problem, thus making the preconditioning system solvable using multigrid in contrast to the original Helmholtz problem. Recently a variation on CSL by the name of Complex Stretched Grid (CSG) was proposed [2], introducing a complex valued grid distance (complex rotation) in the preconditioner.
The far field map computation proposed in this work reformulates the standard real-valued Green's function integral expression for the far field amplitude on a complex contour. Hence, one requires the solution of the Helmholtz equation on a complex contour. It is shown that the latter problem is equivalent to a CSL problem that can be solved very efficiently using a multigrid method. However, whereas CSL was previously only used as a preconditioner, the proposed complex-valued far field map calculation effectively allows for multigrid to be used as a solver.
The far field map for Helmholtz problems.
The Helmholtz equation is a mathematical representation of the physics
behind a wave scattering at an object ![]() located within a domain
located within a domain
![]() . The equation is
. The equation is
Calculation on a complex contour.
The above far field integral expression can be split into a sum of two
contributions
![]() , where
, where
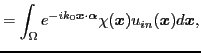 |
(6) | |
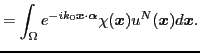 |
(7) |
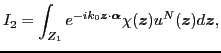 |
(8) |
References.
[1] Y.A. Erlangga, C.W. Oosterlee and C. Vuik, On a class of preconditioners for solving the Helmholtz equation, App. Num. Math., 50(3-4), 2004, pp. 409-425.
[2] B. Reps, W. Vanroose and H. bin Zubair, On the indefinite Helmholtz equation: Complex stretched absorbing boundary layers, iterative analysis, and preconditioning, J. Comput. Phys., 229(22), 2010, pp. 8384-8405.
[3] S. Cools, B. Reps and W. Vanroose, An efficient multigrid calculation of the far field map for Helmholtz problems, arXiv:1211.4461.