


Next: About this document ...
Benjamin Müller
Least-Squares FEM for nonlinear elasticity problems
Institute for Applied Mathematics
Gottfried Wilhelm Leibniz University Hannover
Welfengarten 1
D-30167 Hannover
Germany
bmueller@ifam.uni-hannover.de
Gerhard Starke
Jörg Schröder
Alexander Schwarz
Elastic deformation processes play an important role in solid mechanics.
In this talk, we consider nonlinear elastic behavior with a hyperelastic
material law. Combined with the equations of equilibrium this forms a
nonlinear first order system of partial differential equations for the
displacement 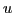 and the first Piola-Kirchhoff stress tensor
and the first Piola-Kirchhoff stress tensor 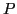 . In
order to solve this system, we consider a nonlinear least squares
functional, which has to be minimized. For the minimization we use the
iterative Gauss-Newton method, which results in a sequence of linear
least squares problems.
. In
order to solve this system, we consider a nonlinear least squares
functional, which has to be minimized. For the minimization we use the
iterative Gauss-Newton method, which results in a sequence of linear
least squares problems.
For the finite element approximation of the associated variational
problem we use quadratic Raviart-Thomas elements for the stress and
continuous quadratic finite elements for the displacement.
At the end of the talk we will give a numerical example and an outlook.
root
2012-02-20