


Next: About this document ...
Misha Kilmer
Tensor-diamond Approximation for Construction of Kronecker Product-based Preconditioners
Dept of Mathematics
Tufts University
503 Boston Ave
Medford
MA 02155
misha.kilmer@tufts.edu
Tamara Kolda
Tensor-diamond Approximation for Construction of Kronecker
Product-based Preconditioners
Suppose 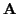 is a square, invertible, block
is a square, invertible, block
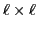 matrix
with
matrix
with
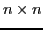 blocks, that is characterized by either (or both) of
the following
conditions:
blocks, that is characterized by either (or both) of
the following
conditions:
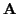 is block Toeplitz (or can be permuted to be block Toeplitz);
is block Toeplitz (or can be permuted to be block Toeplitz);
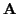 has small block-bandwidth
has small block-bandwidth
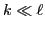 (or, more generally,
the number of non-zero blocks is much less than
(or, more generally,
the number of non-zero blocks is much less than 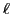 ).
).
Such matrices might arise, for example, in image deblurring or
discretization of a PDE. In this talk, we will primarily focus on
on image deblurring applications.
We consider the problem of determining an approximation 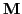 to
to 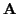 such that either
such that either
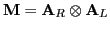
or
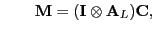
where 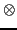 denotes the Kronecker product, and
denotes the Kronecker product, and
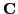 is a matrix
with circulant blocks.
The leftmost problem has been studied previously (see, for example, [1,2]).
Our approach differs from previous approaches in that we produce the
desired factorization by representing
the approximation problem as a third-order tensor (i.e. 3D array) approximation problem.
In the context of PDEs, the approximation
is a matrix
with circulant blocks.
The leftmost problem has been studied previously (see, for example, [1,2]).
Our approach differs from previous approaches in that we produce the
desired factorization by representing
the approximation problem as a third-order tensor (i.e. 3D array) approximation problem.
In the context of PDEs, the approximation 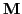 has the advantage of
being relatively easy to directly invert and therefore is attractive as a
preconditioner.
In the context of image deblurring, we can relatively easily compute
rank-revealing factorizations of
has the advantage of
being relatively easy to directly invert and therefore is attractive as a
preconditioner.
In the context of image deblurring, we can relatively easily compute
rank-revealing factorizations of 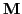 , which can then be used to
generate regularized preconditioners
or surrogate filters, etc.
, which can then be used to
generate regularized preconditioners
or surrogate filters, etc.
Specifically,
we take the relevant descriptive information from 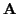 and put this
into an appropriately oriented
and put this
into an appropriately oriented
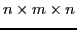 , third-order tensor,
denoted
, third-order tensor,
denoted
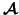 .
We then consider the tensor approximation problem
.
We then consider the tensor approximation problem
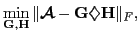
with
possible constraints on
H
where the
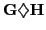 is the product-cyclic tensor, first defined
in [3], given by
is the product-cyclic tensor, first defined
in [3], given by
and
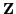 is the
is the
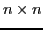 downshift matrix.
We will discuss how the entries of
downshift matrix.
We will discuss how the entries of
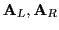 or
or
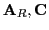 are
constructed from entries in
are
constructed from entries in
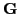 and
and
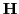 .
.
Numerical results for spatially variant blurring operators show the
possible utility of this approach.
References:
[1] C. F. Van Loan and N. P. Pitsianis, ``Approximation with
Kronecker Products," in Linear Algebra for Large Scale and Real
Time Applications,
Kluwer Publications, 1993, M. S. Moonen and G. H. Golub eds, pages 293-314.
[2] J. Kamm and J. G. Nagy, ``Optimal Kronecker Product
Approximation of Block Toeplitz Matrices," SIAM Journal on Matrix
Analysis and Applications,
volume 22, 2000, pages 155-172.
[3] M. E. Kilmer and T. G. Kolda, ``Approximations of Third Order Tensors as
Sums of (Non-negative) Product Cyclic Tensors," Plenary Presentation,
Householder Symposium, June 2011.



Next: About this document ...
root
2012-02-20
![]() is a square, invertible, block
is a square, invertible, block
![]() matrix
with
matrix
with
![]() blocks, that is characterized by either (or both) of
the following
conditions:
blocks, that is characterized by either (or both) of
the following
conditions:
![]() to
to ![]() such that either
such that either
![]() and put this
into an appropriately oriented
and put this
into an appropriately oriented
![]() , third-order tensor,
denoted
, third-order tensor,
denoted
![]() .
We then consider the tensor approximation problem
.
We then consider the tensor approximation problem