Algorithms based on kernel methods play a central role in statistical
machine learning. At their core are a number of linear algebra operations
on matrices of kernel functions which take as arguments the training and
testing data. A kernel function
![]() generalizes the notion of
the similarity between a test and training point. Given a set of data
points,
generalizes the notion of
the similarity between a test and training point. Given a set of data
points,
![]() , the kernel
matrix is given by,
, the kernel
matrix is given by,
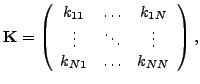 |
(1) |
| (2) |
When the underlying system is ill-conditioned, there is a degradation of
the performance of iterative approaches, necessitating the use of a
preconditioner for the Krylov iterations. Popular preconditioners like
Jacobi, SSOR, ILU can be used to improve the convergence, however, these
preconditioners have an O(![]() ) space and computation requirement for
dense matrices, which would ruin any advantage gained by the fast
matrix-vector products. The preconditioner must have a representation
that allows for a fast matrix-vector product just like the kernel matrix.
We propose a Tikhonov regularized kernel matrix solved with a
truncated conjugate gradient algorithm as a preconditioner for the kernel
matrix, which can be accelerated using the aforementioned approaches.
Because the symmetry of this preconditioner cannot be guaranteed, we use
a flexible GMRES (Saad,
) space and computation requirement for
dense matrices, which would ruin any advantage gained by the fast
matrix-vector products. The preconditioner must have a representation
that allows for a fast matrix-vector product just like the kernel matrix.
We propose a Tikhonov regularized kernel matrix solved with a
truncated conjugate gradient algorithm as a preconditioner for the kernel
matrix, which can be accelerated using the aforementioned approaches.
Because the symmetry of this preconditioner cannot be guaranteed, we use
a flexible GMRES (Saad, ![]() ) algorithm.
) algorithm.
A good preconditioner will improve the convergence of the iterative
approach at the expense of an increased cost per iteration. The
convergence with proposed preconditioner is shown to be an order of
magnitude better than the unpreconditioned approach. But, for a
preconditioner to be useful, the total time taken by the preconditioned
approach should be less than the unpreconditioned approach. This is
achieved by using the the fast matrix-vector product algorithms,
resulting in a computationally efficient solver with faster convergence.
We use two classes of fast matrix vector products, approximation-based
acceleration (eg. FIGTREE (Morariu et al., ![]() ) for Gaussian kernel)
and GPU-based parallelization (Srinivasan et al,
) for Gaussian kernel)
and GPU-based parallelization (Srinivasan et al, ![]() ). Each of these
two approaches have their own advantages and disadvantages. We propose a
strategy to choose the appropriate acceleration in the light of the
desired accuracy.
). Each of these
two approaches have their own advantages and disadvantages. We propose a
strategy to choose the appropriate acceleration in the light of the
desired accuracy.
The performance is further illustrated in popular learning approaches
namely, radial basis function interpolation, Gaussian process regression
and kernel classification. There is an improvement of upto ![]() X in
the number of iterations to converge and
X in
the number of iterations to converge and ![]() X in the total time
taken compared to a conjugate gradient based approach. The core
preconditioning strategy proposed here will soon be released as an open
source package.
X in the total time
taken compared to a conjugate gradient based approach. The core
preconditioning strategy proposed here will soon be released as an open
source package.