Stochastic preconditioning for iterative linear equation solvers

Haifeng Qian
Dept. of Electrical and Computer Engineering, 200 Union Street SE
University of Minnesota, Minneapolis MN 55455
qianhf@ece.umn.edu
Sachin Sapatnekar

Stochastic techniques, namely random walks, have been used to form linear equation solvers since the 1940s, but have not been used effectively for preconditioning, to the best of our knowledge. In this talk, we present a new stochastic preconditioning approach: we prove that for symmetric diagonally-dominant M-matrices, an incomplete LDL factorization can be obtained from random walks, and used as a preconditioner for an iterative solver, e.g., conjugate gradient. The theory can be extended to general matrices with nonzero diagonal entries.

The stochastic preconditioning is performed by a random walk ``game'' defined as follows. Given a finite undirected connected graph representing a street map, a walker starts from one of the nodes, and goes to one of the adjacent nodes every day with a certain probability. The walker pays an amount of money, $ m_i$ at node $ i$, to a motel for lodging everyday, until he/she reaches one of the homes, which are a subset of the nodes. Then the journey is complete and he/she will be rewarded a certain amount of money, $ m_0$. The problem is to determine the gain function:

$\displaystyle f(i)=E[\textrm{money earned }\vert \textrm{walk starts at node }i] $

These gain values satisfy the following linear equations:
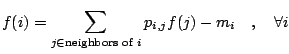    $\displaystyle f(i)=\sum_{j \in \textrm{neighbors of }i}{p_{i,j}f(j)}-m_i \quad,\quad \forall i$  
    $\displaystyle f(\textrm{a home node}) = m_0$  

where $ p_{i,j}$ is the transition probability of going from node $ i$ to node $ j$, and note that $ j$ can be a home node. Thus a random walk game is mapped onto a system of linear equations. Conversely, it can be verified that given $ A \mathbf{x} = \mathbf{b}$, where $ A$ is a symmetric diagonally-dominant M-matrix, we can always construct a random walk game that is mathematically equivalent, in which the set of $ f$ values is equal to the solution vector $ \mathbf{x}$. To find the $ i^{\rm th}$ entry of $ \mathbf{x}$, one may run a number of walks from node $ i$ and take the average of the results; to get the complete solution, one may repeat the process for every entry of $ \mathbf{x}$. We alter this normal procedure by adding the following rule: every calculated node becomes a new home in the game with an award amount equal to its calculated $ f$ value. Without loss of generality, suppose the nodes are in the natural ordering $ 1,2,\cdots,N$, then for walks starting from node $ i$, the node set $ \{1,2,\cdots,i-1\}$ are homes where walks terminate (in addition to homes generated from the strictly-diagonally-dominant rows of $ A$), while the node set $ \{i,i+1,\cdots,N\}$ are motels where walks pass by.

Define the operator $ {\rm rev}(\cdot)$ on square matrices such that it reverses the ordering of the rows and reverses the ordering of the columns: $ {\rm rev}(A)_{i,j}=A_{N+1-i,N+1-j} , \quad \forall i,j \in \{ 1,2,\cdots,N \}$. Let the exact LDL factorization of $ {\rm rev}(A)$ be $ {\rm rev}(A) = L_{{\rm rev}(A)} D_{{\rm rev}(A)} \left( L_{{\rm rev}(A)} \right)^{\rm T}$. Again, in the random walk game, assume that the nodes are in the natural ordering $ 1,2,\cdots,N$, and that node $ i$ corresponds to the $ i^{\rm th}$ row of $ A$. We prove the following relations:

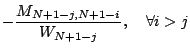$\displaystyle \left( L_{{\rm rev}(A)} \right)_{i,j}$ $\displaystyle \approx$ $\displaystyle - \frac{M_{N+1-j,N+1-i}}{W_{N+1-j}}, \quad\forall i>j$  
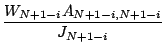$\displaystyle \left( D_{{\rm rev}(A)} \right)_{i,i}$ $\displaystyle \approx$ $\displaystyle \frac{W_{N+1-i} A_{N+1-i,N+1-i}} {J_{N+1-i}}$  

where $ W_k$ is the total number of walks that are carried out from node $ k$, $ M_{k_1,k_2}$ is the number of walks that start from node $ k_1$ and end at $ k_2$, and $ J_{k}$ is the number of times that the $ W_k$ walks from node $ k$ pass node $ k$ itself. These equations show that we can approximate an LDL factorization by collecting information from random walks. We further prove that if $ \left( L_{{\rm rev}(A)} \right)_{i,j} = 0$ then $ M_{N+1-j,N+1-i} = 0$; in other words, the nonzero pattern of the $ L$ factor produced by random walks is a subset of nonzero pattern of the exact $ L_{{\rm rev}(A)}$. Therefore, we conclude that an incomplete LDL factorization can be obtained from random walks.

We argue that the obtained incomplete LDL factors have better quality, i.e., better accuracy-size tradeoffs, than the incomplete Cholesky factor obtained by a traditional method based on Gaussian elimination. Our argument is based on the fact that each row in the $ L$ factor is independently calculated and has no correlation with the computation of other rows. Therefore we avoid the error accumulation in traditional incomplete factorization procedure.

We also discuss, by defining a new set of game rules, how this theory can be extended to general matrices, given that the diagonal entries are nonzero.

To evaluate the proposed approach, a set of benchmark matrices are generated by Y. Saad's SPARSKIT by finite-difference discretization of the 3D Laplace's equation $ \nabla^2 u = 0$ with Dirichlet boundary condition. The matrices correspond to 3D grids with sizes $ 50\times 50\times 50$, $ 60\times 60\times 60$, up to $ 100\times 100\times 100$, and a right-hand-side vector with all entries being 1 is used with each of them. We compare the proposed solver, i.e., random walk preconditioned conjugate gradient, against ICCG with ILU(0) and ICCG with ILUT. The complexity metric is the number of double-precision multiplications needed at the iterative solving stage, in order to converge with an error tolerance of $ 10^{-6}$. The results show up to 2.1 times speedup over ICCG, and a trend that the larger and denser a matrix is, the more the proposed solver outperforms ICCG.

This talk is partially based on [1], and the implementation is available to the public [2].

[1] H. Qian, S. S. Sapatnekar, A hybrid linear equation solver and its application in quadratic placement, IEEE/ACM International Conference on Computer Aided Design Digest of Technical Papers (2005) 905-909.

[2] H. Qian, S. S. Sapatnekar, The Hybrid Linear Equation Solver Binary Release, available at http://www.ece.umn.edu/users/qianhf/hybridsolver