A mathematical framework for equivalent real formulations

Sarah M. Knepper
37 N College Ave, Box 787
Saint Joseph MN 56374
smknepper@csbsju.edu
Michael A. Heroux

Equivalent real formulations (ERFs) are useful for solving complex linear systems using real solvers. Using the four ERFs discussed by Day and Heroux [1], each can be expressed by multiplying the canonical $ K$ form of the complex matrix by certain diagonal and permutation matrices on either side. This will allow, for instance, one ERF to be used as a preconditioner and another ERF to be used to iteratively solve the linear system by simply switching back and forth between the forms through scaling and permuting.

Many real world problems result in a complex-valued linear system of the form $ C w = d$, where $ C$ is a known $ m\times n$ complex matrix, $ d$ is a known $ m\times 1$ complex vector, and $ w$ is an unknown $ n\times 1$ complex vector. We can re-write $ C$ as a real matrix of size $ 2m\times 2n$ called the canonical $ K$ form. If we let matrix $ A$ contain the real parts of the complex matrix $ C$ and let matrix $ B$ consist of the corresponding imaginary parts, we can write $ A + i B = C$. 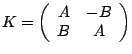The canonical $ K$ form is created by forming the matrix $ K = \left( \begin{array}{cc} A & -B \\ B & A \end{array}\right) $.

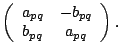To preserve the sparsity pattern of $ C$, each complex value $ c_{pq} = a_{pq} + ib_{pq}$ is converted into a $ 2\times 2$ sub-block with the structure $ \left( \begin{array}{cc} a_{pq} & -b_{pq} \\ b_{pq} & a_{pq} \end{array}\right) .$ For instance, if

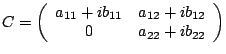
$\displaystyle C = \left( \begin{array}{cc} a_{11} + i b_{11} & a_{12} + i b_{12} \\ 0 & a_{22} + i b_{22} \end{array}\right) $

then the permuted canonical $ K$ form is

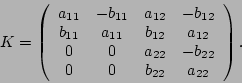
\begin{displaymath}K = \left( \begin{array}{cccc} a_{11} & -b_{11} & a_{12} & -b... ...{22} & -b_{22} \\ 0 & 0 & b_{22} & a_{22} \end{array} \right). \end{displaymath}

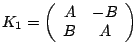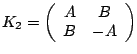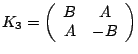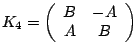The four ERFs that we will concern ourselves with are: $ K_1 = \left( \begin{array}{cc} A & -B \\ B & A \end{array}\right) $, $ K_2 = \left( \begin{array}{cc} A & B \\ B & -A \end{array}\right) $, $ K_3 = \left( \begin{array}{cc} B & A \\ A & -B \end{array}\right) $, and $ K_4 = \left( \begin{array}{cc} B & -A \\ A & B \end{array}\right) $. Each of the ERFs can be obtained from the permuted canonical $ K$ form by multiplying by diagonal and permutation matrices on both sides. In other words, $ K_i = D_l P_l K P_r D_r$, where $ D_l$, $ P_l$, $ P_r$, and $ D_r$ are certain matrices depending on the size of the complex matrix and which ERF we desire. Three diagonal matrices and two permutation matrices (together with their transposes) exist for the ERFs we are considering.

The talk will describe the specific diagonal and permutation matrices needed as well as how to transform from one ERF to another.

[1] David Day and Michael A. Heroux, Solving Complex-Valued Linear Systems via Equivalent Real Formulations, SIAM J. Sci. Comput. 23(2) (2001) 480-498.