The block grade of a block Krylov space

Martin H. Gutknecht
Seminar for Applied Mathematics, ETH Zurich
8092 Zurich, Switzerland
mhg@math.ethz.ch
Thomas Schmelzer

The so-called grade of a vector $ b$ with respect to a nonsingular matrix $ {\mathbf A}$ is the dimension of the (largest) Krylov (sub)space generated by $ {\mathbf A}$ from $ b$. It determines in particular, how many iterations a Krylov space method with linearly independent residuals requires for finding in exact arithmetic the solution of $ {\mathbf A}x=b$ (if the initial approximation $ x_0$ is the zero vector). In this talk we generalize the grade notion to block Krylov spaces and show that this and other fundamental properties carry over to block Krylov space methods for solving linear systems with multiple right-hand sides.

We consider $ s$ linear systems with the same nonsingular coefficient matrix $ {\mathbf A}$, but different right-hand sides $ b^{(i)}$, which we gather in a block vector $ {\mathbf b}:= (b^{(1)},\dots,b^{(s)})$. The $ s$ systems are then written as

$\displaystyle {\mathbf A}{\mathbf x}= {\mathbf b}$   with$\displaystyle \quad {\mathbf A}\in \mathbb{C}^{N\times N}\,, \quad {\mathbf b}\in \mathbb{C}^{N\times s}\,,\quad {\mathbf x}\in \mathbb{C}^{N\times s}\,. $

Standard block Krylov space methods construct in the $ n$th iteration approximate solutions gathered in a block vector $ {\mathbf x}_n$ chosen such that

$\displaystyle {\mathbf x}_n - {\mathbf x}_0 \in {\mathcal B}^{\Box}_n ({\mathbf A}, {\mathbf r}_0) \,, $

where $ {\mathbf x}_0$ contains the $ s$ initial approximations and $ {\mathbf r}_0$ the corresponding initial residuals, while $ {\mathcal B}^{\Box}_n$ is the Cartesian product

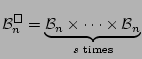
$\displaystyle {\mathcal B}^{\Box}_n = \underbrace{{\mathcal B}_n \times \cdots \times {\mathcal B}_n}_{s\text{ times}} $

with

$\displaystyle {\mathcal B}_n = \mathcal{K}_n ({\mathbf A}, r_0^{(1)}) + \cdots + \mathcal{K}_n ({\mathbf A}, r_0^{(s)}) \,. $

Here, $ \mathcal{K}_n ({\mathbf A}, r_0^{(i)})$ is the usual $ n$th Krylov (sub)space of the $ i$th system. It is important, that, in general, the sum in the last formula is not a direct sum, that is, the Krylov spaces may have nontrivial intersections.

The block grade of $ {\mathbf r}_0$ with respect to $ {\mathbf A}$ or, the block grade of $ {\mathbf A}$ with respect to $ {\mathbf r}_0$ is the positive integer $ \bar\nu := \bar\nu({\mathbf r}_0,{\mathbf A})$ defined by

$\displaystyle \bar\nu({\mathbf r}_0,{\mathbf A}) = \min \left\{n \big\vert \mat... ...hop{\mathrm{dim\ }} {\mathcal B}_{n+1}({\mathbf A}, {\mathbf r}_0) \right\}\,. $

Among the results we have established for the block grade are the following ones.

LEMMA 1  For $ n \geq \bar\nu({\mathbf r}_0,{\mathbf A})$,

$\displaystyle {\mathcal B}_n({\mathbf A}, {\mathbf r}_0) = {\mathcal B}_{n+1}({... ... A}, {\mathbf r}_0) = {\mathcal B}^{\Box}_{n+1}({\mathbf A}, {\mathbf r}_0)\,. $

LEMMA 2  The block grade of the block Krylov space and the grades of the individual Krylov spaces contained in it are related by

$\displaystyle {\mathcal B}_{\bar\nu({\mathbf r}_0,{\mathbf A})}({\mathbf A}, {\... ...dots + \mathcal{K}_{\bar\nu(r_0^{(s)},{\mathbf A})}({\mathbf A}, r_0^{(s)})\,. $

LEMMA 3  The block grade $ \bar\nu({\mathbf r}_0,{\mathbf A})$ is characterized by

$\displaystyle \bar\nu({\mathbf r}_0,{\mathbf A}) = \min\left\{ n \big\vert {\ma... ... {\mathbf r}_0 \in {\mathcal B}^{\Box}_n({\mathbf A}, {\mathbf r}_0) \right\}. $

THEOREM  Let $ {\mathbf x}_{\mbox{\scriptsize $\star$}}$ be the block solution of $ {\mathbf A}{\mathbf x}= {\mathbf b}$ and let $ {\mathbf x}_0$ be any initial block approximation of it and $ {\mathbf r}_0 := {\mathbf b}- {\mathbf A}{\mathbf x}_0$ the corresponding block residual. Then

$\displaystyle {\mathbf x}_{\mbox{\scriptsize $\star$}}\in {\mathbf x}_0 + {\mat... ... B}^{\Box}_{\bar\nu({\mathbf r}_0,{\mathbf A})}({\mathbf A},{\mathbf r}_0) \,. $

We also discuss the effects of the size of the block grade on the efficiency of a block Krylov space method.