A note on GMRES preconditioned by a perturbed
$ LDL^T$ decomposition with static pivoting

Iain S Duff
Rutherford Appleton Laboratory, Chilton, Didcot
Oxfordshire, OX11 0QX, UK
i.s.duff@rl.ac.uk
Mario Arioli, Serge Gratton, Pralet, Stéphane

This paper is concerned with solving the set of linear equations $ A x = b$ (1) where the coefficient matrix $ A$ is a symmetric indefinite sparse matrix. Our hope is to solve this system using a direct method that uses an accurate factorization of $ A$ but sometimes the cost of doing this is too high in terms of time or memory. We have therefore looked at the possibility of using static pivoting to avoid these problems which are particularly acute if the matrix is highly indefinite as for example can happen for saddle-point problems.

As our direct method we will use a multifrontal approach. In this approach we first determine an order for choosing pivots based on the sparsity structure of $ A$ (called the analysis step), and we then accommodate further pivoting for numerical stability during the subsequent numerical factorization phase. The problem when the matrix is highly indefinite is that the resulting pivot sequence used in the numerical factorization can differ substantially from that predicted by the analysis step. 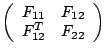In the multifrontal context, the factorization can be represented by a tree at each node of which elimination operations are performed on a partially summed frontal matrix $ \left( \begin{array}{cc} F_{11} & F_{12} \\ F_{12}^T & F_{22} \end{array}\right) $ (2) and pivots at that stage can only be chosen from within the fully summed block $ F_{11}$. The problem occurs when it is impossible or numerically suicidal to eliminate all of $ F_{11}$ resulting in more work and storage (sometimes dramatically more) than forecast. A simple way to avoid this problem is to force the elimination of all of $ F_{11}$ through static pivoting.

We thus assume that the matrix $ A$ has been factorized using the HSL package MA57 with the option of using static pivoting [1]. The static pivoting strategy will set the diagonal entry to $ \pm\tau$ when it is impossible to find a suitable pivot in the fully summed blocks. It is common to choose $ \tau \approx \sqrt{{{\bf\varepsilon }\,}} \vert\vert A\vert\vert$ ( $ {{\bf\varepsilon }\,}$ machine precision).

Therefore, the computed factors $ \hat{L}$ and $ \hat{D}$ are, in exact arithmetic, the exact factorization of the perturbed problem $ A + E = \hat{L} \hat{D} \hat{L}^T$ (3), where the matrix $ \vert E\vert \le \tau I$ is a diagonal matrix of rank equal to the number of static pivots used during the factorization. The nonzero diagonal entries in $ E$ correspond to the positions at which static pivoting was performed and they are all equal to $ \tau$ in modulus. Note that if $ \tau$ is chosen too small then the factorization could be very unstable whereas if it is chosen too large, the factorization will be stable but will not be an accurate factorization of the original matrix (that is, $ \vert E\vert$ will be large).

Equation (3) gives a splitting of $ A$ in terms of $ M = \hat{L} \hat{D} \hat{L}^T$ and $ E$, $ A = M - E$, and the solution of (1) can be expressed as the solution of the equivalent system $ (I - M^{-1} E) x = M^{-1}b$ (4). If the spectral radius of the matrix $ I - M^{-1} E $ is less than one, the system (4) can be solved using iterative refinement. This has been used by many authors, including [1] and is successful over a wide range of matrices although is somewhat sensitive to the value of $ \tau$. If, however, the spectral radius is greater or equal to one (or $ \approx 1$), it is necessary to switch to a more powerful method like GMRES. Although the matrix is symmetric, we choose GMRES since it gives us much more freedom to work with a wide range of preprocessors and preconditionings.

We have found experimentally that using the factorization (3) as a preconditioning for GMRES works in most cases and is, as expected much more robust than iterative refinement. Indeed GMRES gives normwise backward stability in most cases, which is not the case for iterative refinement. However, there are cases where we do not get convergence to a scaled residual at machine precision.

We have, however, found that restarted GMRES performs better and that using FGMRES, even though our preconditioner remains constant, does even better.

We illustrate this through numerical experiment and then show theoretically that, under reasonable assumptions, FGMRES preconditioned by our static pivoting factorization is backward stable so that a small scaled residual can be achieved. Our analysis also holds for the case of restarted FGMRES that we advocate as a measure to control the memory requirement while still achieving the desired accuracy. Indeed we give theoretical arguments why the restarting often greatly improves the convergence.

[1] I. S. Duff and S. Pralet, Towards a stable static pivoting strategy for the sequential and parallel solution of sparse symmetric indefinite systems, Technical Report TR/PA/05/26, CERFACS, Toulouse, France, 2005. (Also available as RAL Report RAL-TR-2005-007 and IRIT Report RT/TLSE/05/04.)