


Next: About this document ...
Matthew Parno
Population based optimization of mixed-variable problems with applications in hydrology
235 Albany St
Apartment 3073
Cambridge
MA 02139
mparno@mit.edu
Many difficult engineering optimization problems involve both continuous
and discrete variables. Additionally, some problems may have discrete
variables that alter the dimension of the continuous problem. Formally,
this work considers problems of the form
where
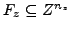 ,
,
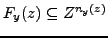 , and
, and
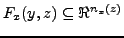 . The variables in
. The variables in 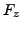 and
and 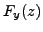 do
not need to be ordered and can be categorical. In general, the continuous
problem
do
not need to be ordered and can be categorical. In general, the continuous
problem
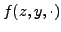 will be nonsmooth and derivatives will not be
available. Thus, current algorithms alternate local searches with
derivative free optimization algorithms on the continuous variables with
a local search of the discrete parameters However, the continuous problem
can often be noisy with many local minima.
will be nonsmooth and derivatives will not be
available. Thus, current algorithms alternate local searches with
derivative free optimization algorithms on the continuous variables with
a local search of the discrete parameters However, the continuous problem
can often be noisy with many local minima.
To this end, we review the existing framework and demonstrate that a
population based algorithm can also be used as a more robust continuous
optimization algorithm. Numerical results are given for several academic
problems as well as a hydraulic capture problem from hydrology.



Next: About this document ...
root
2010-03-02