A novel high-order-accurate, fully-implicit solution algorithm for
all-speed, Navier-Stokes equations is introduced. It combines the
``recovery Discontinuous Galerkin'' (rDG) method for spatial
discretization of the hyperbolic and diffusion operators with the
``Explicit, Singly Diagonal Implicit Runge-Kutta'' (ESDIRK)
scheme for time integration. Both algorithms are implemented under the
``Jacobian-free Newton-Krylov'' (JFNK) framework. Since
hyperbolic and diffusion operators are fully-coupled, temporal
discretization errors due to operator-splitting are completely
eliminated. The algorithm is demonstrated to be high-(up to
![]() )-order time-accurate in a wide range of Mach, Reynolds and
Péclet numbers even when the pressure-gradient, viscous and
heat-conduction operators become of comparable size. The rDG formulation
exhibits nearly-spectral accuracy (shown up to the
)-order time-accurate in a wide range of Mach, Reynolds and
Péclet numbers even when the pressure-gradient, viscous and
heat-conduction operators become of comparable size. The rDG formulation
exhibits nearly-spectral accuracy (shown up to the ![]() -order) in
space. The Newton-Krylov (NK) solution is formulated in conservative
variables (i.e. density,
-order) in
space. The Newton-Krylov (NK) solution is formulated in conservative
variables (i.e. density, ![]() ; total energy,
; total energy, ![]() ; and momentum,
; and momentum, ![]() ),
which allows one to stop Newton's iteration any time (if locked in the
limit cycle) without loosing conservation. The ESDIRK and rDG
discretizations provide natural utilities to compute a high-order error
estimate in both time and space, which is especially beneficial for
Adaptive Mesh Refinement (AMR) and time step control.
),
which allows one to stop Newton's iteration any time (if locked in the
limit cycle) without loosing conservation. The ESDIRK and rDG
discretizations provide natural utilities to compute a high-order error
estimate in both time and space, which is especially beneficial for
Adaptive Mesh Refinement (AMR) and time step control.
The main challenge is to ensure the efficiency of the JFNK linear solver, for which we employ the Jacobian-free version of the right-preconditioned GMRES method. The focus of this paper is the Physics-Based Preconditioning (PBP) of our rDG-JFNK algorithm. It is designed to ``cluster'' eigenvalues of the Jacobian matrix, ensuring convergence of the GMRES within a few Krylov iterations. Two PBP strategies, specifically designed for DG-type of spatial discretizations, are introduced and extensively tested.
The first PBP capitalizes on explicit availability of the
higher-order derivatives in the DG local solution vector. The Jacobian
matrix
![]() can be rearranged in the block-vector form. Each
element
can be rearranged in the block-vector form. Each
element
![]() of the Jacobian matrix
of the Jacobian matrix
![]() is a
is a
![]() matrix, and p is the highest order of the basis
functions, representing non-local coupling of solutions between
matrix, and p is the highest order of the basis
functions, representing non-local coupling of solutions between ![]() and
and ![]() cells (i.e.
cells (i.e.
![]() and
and
![]() ).
).
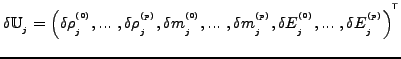 is a local solution
vector at cell j. Elimination of the off-diagonal blocks
is a local solution
vector at cell j. Elimination of the off-diagonal blocks
![]() can be
interpreted as freezing the nonlocal coupling at the previous Newton
iteration. When used for preconditioning, this block-diagonal
approximation not only provides a tight coupling of the local solution
vector (which is very effective when the reaction terms are stiff), but
also takes into account some non-local coupling since the
spatial derivatives are the part of the local solution vector. We refer
to this as ``Block-Diagonal''(BD) preconditioner, and its
efficiency is demonstrated here in terms of a) the patterns of
eigenvalues for the Jacobian matrix (``Eigenscopy''); and
b) the number of the Krylov iterations/vectors required to
converge the GMRES to a given linear tolerance.
can be
interpreted as freezing the nonlocal coupling at the previous Newton
iteration. When used for preconditioning, this block-diagonal
approximation not only provides a tight coupling of the local solution
vector (which is very effective when the reaction terms are stiff), but
also takes into account some non-local coupling since the
spatial derivatives are the part of the local solution vector. We refer
to this as ``Block-Diagonal''(BD) preconditioner, and its
efficiency is demonstrated here in terms of a) the patterns of
eigenvalues for the Jacobian matrix (``Eigenscopy''); and
b) the number of the Krylov iterations/vectors required to
converge the GMRES to a given linear tolerance.
The second PBP incorporates non-local effects. We split
preconditioning into three steps, each targeting eigenvalues associated
with a specific physics (i.e., heat conduction, stiff pressure waves and
viscous operator). First, we transform the NK solution vector from
conservative variables to primitive variables (i.e., pressure, ![]() ;
velocity,
;
velocity, ![]() : and internal energy,
: and internal energy, ![]() ). A consistent transformation of
the higher order derivatives is carried out by enforcing the conservation
in the weak sense. The resulting system can be cast into the following
block-vector form,
). A consistent transformation of
the higher order derivatives is carried out by enforcing the conservation
in the weak sense. The resulting system can be cast into the following
block-vector form,
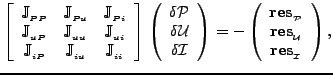
where each element
![]() is a
is a
![]() matrix, representing non-linear
coupling between the
matrix, representing non-linear
coupling between the ![]() and
and ![]() primitive variables.
primitive variables.
In order to solve this coupled system, we first decouple the internal
energy from the pressure-velocity matrix, solving for
![]() .
Step I targets the heat conduction operator. Next, we formulate the
pressure-Poisson equation as
.
Step I targets the heat conduction operator. Next, we formulate the
pressure-Poisson equation as
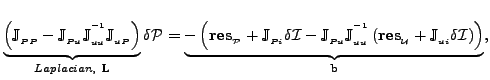
where the Laplacian can be shown to be closely related to the Schur complement of the pressure-velocity matrix. This parabolic system can be solved efficiently using a multigrid method. Step II targets stiff pressure waves. Finally, we solve for velocity, accounting for viscous stress terms. In the 1D representation, this Step III can be written as
It can be easily seen that this PBP is closely related to the classical
``operator-split'' solution algorithms for incompressible and
weakly-compressible flows (e.g., ICE, SIMPLE, Projection). Therefore, we
referred to this as ``Operator-Split'' (OS) preconditioner. We
demonstrate that the OS preconditioner is very effective in clustering
generally-complex eigenvalues near the real axis. It is also found to be
very effective in a wide range of Mach (![]() ) and Reynolds (
) and Reynolds (![]() ) numbers,
keeping the number of GMRES iterations
) numbers,
keeping the number of GMRES iterations ![]() , even at the extremes of
, even at the extremes of
![]() and very low
and very low ![]() numbers.
numbers.