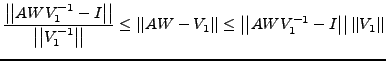Next: Bibliography
Marko Huhtanen
APPROXIMATE FACTORS FOR THE INVERSE
Institute of Mathematics
Helsinki University of Technology
Box 1100
FIN-02015
Finland
marko.huhtanen@tkk.fi
Let
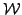 and
and
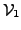 be sparse matrix subspaces
of
be sparse matrix subspaces
of
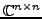 containing
invertible elements such that those
of
containing
invertible elements such that those
of
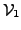 are readily invertible.
To precondition a large linear system involving
a sparse nonsingular matrix
are readily invertible.
To precondition a large linear system involving
a sparse nonsingular matrix
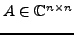 ,
in this talk we consider
,
in this talk we consider
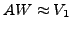 |
(1) |
with non-zero matrices
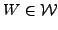 and
and
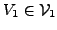 both regarded as variables.
The attainability of the possible equality
can be
verified by inspecting the nullspace of
both regarded as variables.
The attainability of the possible equality
can be
verified by inspecting the nullspace of
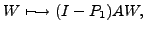 with with 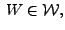 |
(2) |
where 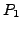 is the orthogonal
projection onto
is the orthogonal
projection onto
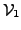 [1].
[1].
Corresponding to the smallest singular values of (![[*]](file:/usr/share/latex2html/icons/crossref.png) ),
we have
),
we have
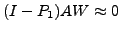 if and only if
if and only if
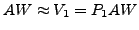 .
This gives rise to the criterion
.
This gives rise to the criterion
for a starting point to generate approximate
factors 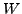 and
and 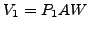 . Then
in the 2-norm,
whenever
. Then
in the 2-norm,
whenever 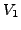 is invertible.
Consequently,
the maximum gap between these two approximation problems
is determined the condition number of
is invertible.
Consequently,
the maximum gap between these two approximation problems
is determined the condition number of 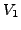 .
In the special case
.
In the special case
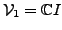 the equalities hold in general. This corresponds
to the criterion
which constitutes a starting point for constructing
sparse approximate inverses.
the equalities hold in general. This corresponds
to the criterion
which constitutes a starting point for constructing
sparse approximate inverses.



Next: Bibliography
Marian
2008-02-26
![]() and
and
![]() be sparse matrix subspaces
of
be sparse matrix subspaces
of
![]() containing
invertible elements such that those
of
containing
invertible elements such that those
of
![]() are readily invertible.
To precondition a large linear system involving
a sparse nonsingular matrix
are readily invertible.
To precondition a large linear system involving
a sparse nonsingular matrix
![]() ,
in this talk we consider
,
in this talk we consider
![]() ),
we have
),
we have
![]() if and only if
if and only if
![]() .
This gives rise to the criterion
.
This gives rise to the criterion