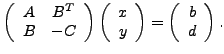Sue Dollar
Equivalent SPD systems for saddle-point problems

Rutherford Appleton Laboratory
Chilton
Oxfordshire
OX11 0QX
s.dollar@rl.ac.uk
Nick Gould
Martin Stoll
Andy Wathen

Consider symmetric saddle-point problems of the form

$$\left( \begin{array}{cc} A & B^T \\ B & -C \end{array} \right) \l... ...x \\ y \end{array} \right) =\left( \begin{array}{c} b \\ d \end{array} \right).$$ (1)

The solution to () also satisfies the symmetric system

$$\left[ \sigma \left( \begin{array}{cc} A & B^T \\ B & -C \end{arr... ... \end{array} \right) \right] \left( \begin{array}{c} x \\ y \end{array} \right)$$ (2)

$$= \left( \begin{array}{c} \sigma b + A(Db + F^T d) + B^T ( F b + E d) \\ \sigma d + B(D b + F^T d) - C (F b - E d) \end{array} \right),$$

for given real $\sigma,$ arbitrary symmetric matrices $D$ and $E,$ and arbitrary matrix $F.$

We show that many popular conjugate gradient-based methods for solving () can be reformulated as applying the (preconditioned) conjugate gradient method to () for some $\sigma,$ $D,$ $E$ and $F.$ We also provide conditions for guaranteeing that () is positive definite. Using these conditions we propose new conjugate gradient-based methods for solving () and give numerical results for problems from optimization and fluid dynamics.