| (1) |
The solution of a large size sparse linear system of equations
| (1) |
In this paper, two new preconditioners built upon the dynamic FSAI algorithm [Janna et al., 2015] are considered: the BTFSAI - Block Tridiagonal Factorized Sparse Approximate Inverse - and the DDFSAI - Domain Decomposition Factorized Sparse Approximate Inverse. The first one is based on the successive application of the FSAI algorithm on the matrix reordered in a block tridiagonal structure and the second one is based on the combination of a two level domain decomposition approach and the FSAI preconditioner, which is used for computing the approximate inverse of the inner submatrices and the Schur complement.
In the Block Tridiagonal preconditioner - BTFSAI - the matrix
![]() is first
reordered by the reverse Cuthill-McKee algorithm, with the aim to reduce its bandwidth,
and then it is divided into a block tridiagonal structure according to a given number
of blocks. After that, the block LDU decomposition of this new matrix is calculated
where the inverses of the diagonal blocks are approximated explicitly by the adaptive
FSAI algorithm.
is first
reordered by the reverse Cuthill-McKee algorithm, with the aim to reduce its bandwidth,
and then it is divided into a block tridiagonal structure according to a given number
of blocks. After that, the block LDU decomposition of this new matrix is calculated
where the inverses of the diagonal blocks are approximated explicitly by the adaptive
FSAI algorithm.
With this approach, the global matrix is subdivided into small blocks, that should be
approximated with less effort. Though this method is intrinsically sequential,
parallelism can be exploited for each block by the use of the FSAI algorithm.
Calling
![]() the SPD diagonal submatrix and
the SPD diagonal submatrix and
![]() the upper diagonal
submatrix of the
the upper diagonal
submatrix of the ![]() block, the block LDU decomposition reads
block, the block LDU decomposition reads
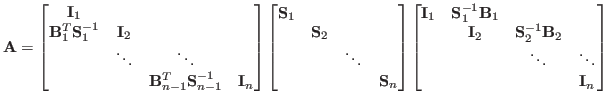 |
(2) |
| (3) |
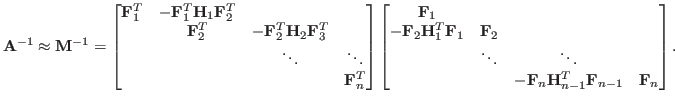 |
(4) |
Roughly speaking, domain decomposition refers to a number of techniques which solve a
problem defined on a large domain ![]() via the solution of smaller problems defined
over subdomains
via the solution of smaller problems defined
over subdomains
![]() . Each problem can be solved independently and
the solutions can be gathered to build the outcome of the original problem.
. Each problem can be solved independently and
the solutions can be gathered to build the outcome of the original problem.
In the domain decomposition FSAI preconditioner - DDFSAI - the graph of the original matrix is reordered according to the k-way partition algorithm implemented in the METIS software library. With this method, the number of edges connecting a subdomain to the others is minimized, thus reducing the pieces of information that need to be communicated among different blocks. At the same time, the size of subdomains is kept to be approximately of the same order in favour of providing a good load balance among different threads, which are going to work in one or possibly more blocks. After this, each independent block of the matrix is reordered according to the reverse Cuthill-McKee algorithm in order to reduce its bandwidth.
The algorithm for constructing the DDFSAI preconditioner is almost the same as BTFSAI restricted to two blocks, with the only difference consisting in the initial ordering of the matrix, which in the current case uses the METIS library besides of the reverse Cuthill-McKee ordering.
The results show that the BTFSAI technique is very promising in terms of decreasing the total number of iterations and time for achieving the solution. Further, with the DDFSAI technique, the computational pain is smaller, but stability and scalability are generally better. We remark that these strategies are under development and further computational improvements are being addressed, for instance a hybrid MPI/OpenMP implementation.